Introduction
These notes are on the COP4533 Algorithm Abstraction & Design with Professor Ungor at the University of Florida. What I have learned from this course has been compounded into these notes.
Stable Matching Problem
-
Given a set of preferences among hospitals and med-school students, we have to design a self-reinforcing admissions process.
-
A matching $M$ is a set of ordered pairs, $h-s$, where $h \in H$ and $s \in S$, such that:
-
Each hospital $h \in H$ appears in at most one pair of $M$.
-
Each student $s \in S$ appears in at most one pair of $M$.
-
-
For a given matching, $M$, it is perfect if $|M| = |H| = |S| = n$
-
Unstable pair: Given a hospital $h$ and a student $s$, they form an unstable pair if both:
-
$h$ prefers $s$ to one of its admitted students.
-
$s$ prefers $h$ to their assigned hospital.
-
-
Stable assignment: A group of pairs, an assignment, in which there is no unstable pairs.
-
Stable matching: A perfect matching with no unstable pairs.
-
Tl;dr given the a list of preferences with $n$ hospitals and $n$ students, return a stable matching.
Input
-
The input to the stable matching problem is a set of $n$ hospitals, $H$, and a set of $n$ students $S$.
-
Each hospital $h \in H$ ranks students.
-
Each student $s \in S$ ranks hospitals.
-
An example:
-
A set of hospitals, $H$ with $n = 2$ students:
- Ranking is in order of preference, i.e. Chicago prefers Coleton over Daniel, but Tampa prefers Daniel over Coleton
| Hospitals | 1st | 2nd |
|---|---|---|
| Chicago | Coleton | Daniel |
| Tampa | Daniel | Coleton |
-
A set of students, $S$ with $n = 2$ hospitals:
- Ranking, just like before, is in order of preference.
| Students | 1st | 2nd |
|---|---|---|
| Coleton | Tampa | Chicago |
| Daniel | Chicago | Tampa |
Perfect Matching
What is a perfect matching for the above table example? It could be:
- $M = \{ \text{Chicago} - \text{Coleton},~ \text{Tampa} - \text{Daniel}\}$
The following is also a perfect matching, but an inverse example:
- $M = \{ \text{Tampa} - \text{Coleton},~ \text{Chicago} - \text{Daniel}\}$
Unstable Pair
-
In the above example, both possible matchings are perfect and lack unstable pairs (i.e. both are stable matchings.)
-
In the first example, although Coleton preferred Tampa and Daniel preferred Chicago, it is still stable as each $h \in H$ recieved a preferred student.
-
In the second example, although Tampa preferred Daniel and Chicago preferred Coleton, it is still stable as each $s \in S$ recieved a preferred hospital.
-
How about an example where this is not the case?
| Hospitals | 1st | 2nd | 3rd |
|---|---|---|---|
| Chicago | Ella | Daniel | Coleton |
| Tampa | Daniel | Coleton | Ella |
| Columbus | Daniel | Ella | Coleton |
| Students | 1st | 2nd | 3rd |
|---|---|---|---|
| Coleton | Tampa | Chicago | Columbus |
| Daniel | Chicago | Tampa | Columbus |
| Ella | Chicago | Columbus | Tampa |
A possible perfect matching for this would be:
- $M = \{ \text{Columbus} - \text{Ella},~\text{Tampa} - \text{Daniel},~\text{Chicago} - \text{Coleton} \}$
A possible unstable pair for $M$ would be $\text{Chicago} - \text{Ella}$, in this case a hospital $h$ (Chicago) prefers matched student $s$ (Ella), and a student $s$ (Ella) prefers matched hospital $h$ (Chicago). This means although the matching is, indeed, perfect, it is not a stable matching.
- The key point: An unstable pair $h - s$ could each improve by a joint action, which we want to avoid.
Stable Roomate Problem
Given a different set of problem, do stable matchings always exist? This question is, even with the prior example of stable matching problem, not exactly obvious.
This brings us to the stable roommate problem:
-
$2n$ people; each person ransk others from $1$ to $2n - 1$.
-
The goal: assign the roommate pairs such that there are no unstable pairs.
Let’s take a look at an example where a stable matching does not exist:
| People | 1st | 2nd | 3rd |
|---|---|---|---|
| Anthony | Bailey | Carl | Darryl |
| Bailey | Carl | Anthony | Darryl |
| Carl | Anthony | Bailey | Darryl |
| Darryl | Anthony | Bailey | Carl |
-
$\text{Anthony}-\text{Bailey},~\text{Carl}-\text{Darryl} \rightarrow \text{Bailey}-\text{Carl}~\text{unstable}$
-
$\text{Anthony}-\text{Carl},~\text{Bailey}-\text{Darryl} \rightarrow \text{Anthony}-\text{Bailey}~\text{unstable}$
-
$\text{Anthony}-\text{Darryl},~\text{Bailey}-\text{Carl} \rightarrow \text{Anthony}-\text{Carl}~\text{unstable}$
-
$\Rightarrow$ No perfect matching is stable.
-
$\Rightarrow$ Stable matchings need not exist.
-
Key point: even changing a little about a problem can cause the conditions to make it impossible to guarantee a criteria.
Gale-Shapley deferred acceptance algorithm
This is a method that guarantees to find a stable matching:
initialize $M$ as empty matching;
while some hospital $h$ is unmatched and hasn’t proposed to every student do
$\quad S \leftarrow$ first student on $h$’s list to whom $h$ has not yet proposed;
$\quad$if $s$ is unmatched then
$\qquad$Add $h-s$ to matching $M$;
$\quad$else if $s$ prefers $h$ to current partner $h'$ then
$\qquad$Replace $h'-s$ with $h-s$ in matching $M$;
$\quad$else
$\qquad s$ rejects $h$;
$\quad$end
end
return stable matching $M$;
Effectively, what this does is iterate as long as a hospital $h$ exists such that it is unmatched and hasn’t ran out of students to propose to. It will grab the first student $s$ that hasn’t been proposed to yet by $h$. This means that as this algorithm continues, it will iterate over 1st, 2nd, etc. for each $h \in H$. Next, a few conditions are checked. If $s$ is unmatched, add the match to our matching $M$. If it is matched but $s$ prefers $h$ over its current partner (i.e. the hospital $h'$ that matched with it previously) replace this old pair $h'-s$ with $h-s$ in $M$. Finally, if $s$ doesn’t prefer $h$ over $h'$ (i.e. both $s$ and $h$ prefer each other) then reject and continue. Finally, return the stable matching.
Proof of Correctness: Termination
Some observations, for one the hospitals always propose in decreasing order of preference (i.e. start with most preferred, then go down). Second, once a student is matched, the student will never become unmatched. At worst, (or best I guess), they will just trade up to a more preferred hospital.
-
Claim: Algorithm terminates after at most $n^2$ iterations of while loop.
-
Proof:
-
There are $n$ students and $n$ hospitals.
-
Each time through the while loop, a hospital $h$ will propose to a new student $s$.
-
Thus, there are at most n^2 possible proposals, and the loop will terminate. $\blacksquare$
-
Proof of Correctness: Perfect Matching
-
Claim: Gale-Shapley outputs a matching $M$.
-
Proof:
-
A hospital will propose only if it is unmatched $\Rightarrow$ matched to $\le 1$ student
-
A student keeps only the best hospital $\Rightarrow$ matched to $\le 1$ hospital
-
-
Claim: With Gale-Shapley, all hospitals will be matched.
-
Proof: [by contradiction]
-
There are $n$ students and $n$ hospitals.
-
Suppose that some hospital $h \in H$ is unmatched once Gale-Shapley terminates.
-
Then, subsequently, because $|H| = |S| = n$, some student $s \in S$ is also unmatched.
-
This means that $s$ was never proposed to.
-
But, $h$ proposes to every student, so $h$ is unmatched. $\Rightarrow\!\Leftarrow$
-
-
Claim: With Gale-Shapley, all students will be matched.
-
Proof: [by counting]
-
There are $n$ students and $n$ hospitals.
-
By previous claim, all $n$ hospitals will be matched.
-
$|H| = |S| = n$
-
Thus, all $n$ students get matched as well. $\blacksquare$
-
Proof of Correctness: Stability
-
Claim: With Gale-Shapley returned matching $M$, there are no unstable pairs.
-
Proof: Consider any pair $h-s$ that is not in $M$. Remember, an unstable pair has to be not in $M$ to prove that it is not a stable matching.
-
Case 1: $h$ never proposed to $s$:
-
Due to the fact that hospitals propose in a decreasing order of preference, $h$ must prefer its Gale-Shapley partner, $s'$, over $s$.
-
$\Rightarrow$ $h-s$ is not unstable.
-
-
Case 2: $h$ proposed to $s$:
-
$s$ must have rejected $h$, either right away or at a subsequent iteration.
-
Due to the fact students only trade up, $s$ must prefer its Gale-Shapley partner, $h'$, over $h$.
-
$\Rightarrow$ $h-s$ is not unstable.
-
-
With either case, any pair $h-s \notin M$ is not unstable. $\blacksquare$
-
Hospital Optimality
- For a given problem, there may be several stable matchings:
| People | 1st | 2nd | 3rd |
|---|---|---|---|
| Anthony | Atlanta | Boston | Chicago |
| Bailey | Boston | Atlanta | Chicago |
| Carl | Atlanta | Boston | Chicago |
| Hospitals | 1st | 2nd | 3rd |
|---|---|---|---|
| Atlanta | Baily | Anthony | Carl |
| Boston | Anthony | Baily | Carl |
| Chicago | Anthony | Baily | Carl |
-
Two stable matchings:
-
First possible stable matching: $\{ \text{Anthony}-\text{Atlanta},~\text{Bailey}-\text{Boston},~\text{Carl}-\text{Chicago} \}$.
-
Second possible stable matching: $\{ \text{Anthony}-\text{Boston},~\text{Bailey}-\text{Atlanta},~\text{Carl}-\text{Chicago} \}$.
-
-
Student $s$ is a valid partner for hospital $h$ if there exists any stable matching in which $h$ and $s$ are matched.
-
Atlanta and Boston are valid partners for Anthony.
-
Atlanta and Boston are valid partners for Bailey.
-
Chicago is the only valid partner for Carl.
-
-
The best valid partner is the most preferred valid partner, i.e. the best valid partner for Anthony is Atlanta.
-
Hospital-optimal assignment: Each hospital receives the best valid partner (i.e. best valid student!)
- Some interesting questions: is such an assignment perfect, and is it even stable?
-
This leads to the claim: All executions of Gale-Shapley yield hospital-optimal assignment.
-
Subsequent corollary: Hospital-optimal assignment is a stable matching :)
-
Proof: [by contradiction]
-
Suppose a hospital is matched with a student other than its’ best valid partner.
-
Hospitals propose in a decreasing order of preference.
- $\Rightarrow$ so, some hospital is rejected by a valid partner during the runtime of Gale-Shapley
-
Let $h$ be first such hospital, and let $s$ be the first valid partner that rejects $h$.
-
Let $M$ be a stable matching where $h$ and $s$ are matched.
-
When $s$ rejects $h$ in Gale-Shapley, $s$ forms (or re-affirms) commitment to a hospital, say $h'$.
- $\Rightarrow$ $s$ prefers $h'$ to $h$. Remember, students trade up.
-
Let $s'$ be partner of $h'$ in $M$.
-
$h'$ had not been rejected by any valid partner (including $s'$) at the point when $h$ is rejected by $s$. This is because this is the first rejection by a valid partner.
-
Thus, $h'$ had not yet proposed to $s'$ when $h'$ proposed to $s$.
- $\Rightarrow$ $h'$ prefers $s$ to $s'$. This is because hospitals propose, again, in a decreasing order of preference.
-
Thus, $h'-s$ is unstable in $M$, which is a contradiction. $\blacksquare$
-
-
In a bit more understandable phrasing, if a stable matching $M = \{h-s, h'-s'\}$, then for it to be stable, $h'$ and $s$ must not prefer each other. Though, $s$ is the first valid partner that rejects a hospital, $h$, in our example. Since this is the first rejection by a valid partner, $h'$ had not been rejected by any valid partner (including $s'$) whenever $h'$ proposed to $s$. This must mean that $h'$ prefers $s$ to $s'$ and as a result, $h'-s$ form an unstable pair in $M$ and contradicts the fact it a stable matching.
-
Student Pessimality
-
Does hospital-optimality come at the expense of the students? Yes!
-
Student-pessimal assignment: The inverse of Hospital-optimal, this means each student receives its worst valid partner.
-
Claim: Gale–Shapley finds student-pessimal stable matching $M^*$.
-
Proof: [by contradiction]
-
Suppose $h-s$ is matched in $M^*$ but $h$ is not the worst valid partner for $s$.
-
There exists stable matching $M$ in which $s$ is paired with a hospital, say $h'$, whom $s$ prefers less than $h$.
- $\Rightarrow~s$ prefers $h$ to $h'$.
-
Let $s'$ be the partner of $h$ in $M$.
-
By hospital-optimality, $s$ is the best valid partner for $h$.
- $\Rightarrow~h$ prefers $s$ to $s'$.
-
Thus, $h-s$ is an unstable pair in $M$, a contradiction. $\blacksquare$
-
-
In a more understandable phrasing, let’s just assume $h-s$ is matched in $M^*$ and that $h$ is not the worst valid partner for $s$. Notice, this does not mean $h$ is the best, just not $s$’ worst. Let’s next assume that there exists a stable matching $M$ such that $M = \{ h'-s,~h-s' \}$ and $s$ prefers $h'$ less than $h$. In this case $s$ must prefer $h$ to $h'$. Note, this means that for it to be unstable, $h$ must also prefer $s$ over $s'$. By previous hospital-optimal, $s$ is the best valid partner of $h$, and that means that does mean that $h$ prefers $s$ to $s'$ and that means $h-s$ is an unstable pair in $M$.
-
Deceit
-
Fact 1: No hospital can improve by lying about its preference list.
-
Fact 2: A devious student can possibly improve by lying.
-
Fact 3: There isn’t a stable-matching algorithm that exists such that truth-telling works for all agents.
Algorithm Analysis
Computational Tractability
Models of computation
Turing machines
-
Deterministic Turing machine, it is a simple and idealistic model.
-
Running time: The number of steps.
-
Memory: The number of tape cells utilized.
-
Caveat: There is no random access of memory.
Word RAM.
-
RAM = Random access memory.
-
Each memory location and input/output cell stores a $w$-bit integer (we assume $w \ge \text{log}_2~n$.)
-
Primitive operations: arithmetic/logic operations, read/write memory, array indexing, following a pointer, conditional, branch… constant time C-style operations ($w = 64$).
-
Running time: The number of primitive operations.
-
Memory: Number of cells utilized.
-
Caveat: At times, need more refined model (e.g. multiplying $n$-bit integers)
-
We just assume they are all the same in this model, a primitive.
-
In Gale-Shapley, we assumed proposals to be a primitive operation.
-
Primitive means zooming out, going deeper is zooming in. There are many things happening under the hood, we have to draw the line at some point regarding what is constant and what isn’t constant. See coastline paradox.
-
A loop is most definitely not a primitive, for instance.
-
Brute Force
-
Brute force: For many nontrivial problems, there is a brute-force search algorithm that solves every possible input via checking every possible solution.
-
Typically takes $2^n$ steps (or worse) for inputs of size $n$.
-
This is unacceptable in practice.
-
-
Example: In the stable matching problem, test all $n!$ perfect matching. This is bad!
Polynomial running time
-
Desirable scaling property: When the input size doubles, the algorithm should slow down by at most by some multiplicative constant factor C.
-
Def: An algorithm is poly-time if the following scaling property holds.
-
There exists constants $a > 0$ and $b > 0$ such that, for every input of size $n$, the algorithm performs $\le a~n^b$ primitive computational steps. Corresponds to $C = 2^b$ .
-
I.e. for an algorithm with a complexity of $\Theta(n^b)$, $C = 2^b$.
-
For example, if given an algorithm with a time complexity of $\Theta(n^4)$, $C = 2^4 = 16$.
-
-
-
This level of slow down is a price we are willing to pay, what we are not willing to pay is factorial complexity (brute force for instance).
-
We say that an algorithm is ``efficient’’ if it has a polynomial running time.
-
Theory: Definition is a relatively insensitive to model of computation.
-
Practice: It works!
-
The poly-time algorithms that people develop have both small constants and small exponents.
-
Breaking through the exponential barrier of brute force into polynomial typically exposes crucial structure for the problem.
-
-
Expectations: Some poly-time algorithms in the wild have galactic constants and/or huge exponents.
-
Q. Which would we prefer: $f(n) = 20n^{120}$ or $g(n) = n^{1 + 0.02 \text{ ln } n}$
-
We’d prefer the latter as in practice it is faster.
-
$f(n) \approx 2.66 \times 10^{37}$.
-
$g(n) \approx 3.02$.
-
Key point: just because an algorithm is polynomial doesn’t mean it is fast, have to look at it on a case-to-case basis.
-
Worst-case analysis
-
Worst case: The running time guarantee for any input size of size $n$.
- Generally captures efficiency in practice.
-
Exceptions: Some exponential-time algorithms are used widely in practice because the worst-case instances don’t arise often.
-
Linear programming: Optimize a function with respect to a bunch of constraints. A lot of problems can be expressed in linear programming.
- See Cohen, Lee, and Song for what worst case time complexity can look for this.
-
Simplex method: The worst case is exponential, but it is so rare it is still used to great effect.
-
Other types of analyses
-
Probabilistic: Expected running time of a randomized, non-deterministic algorithm.
- Example: The expected number of compares to quicksort $n$ elements is $2n~\text{ln}~n$.
-
Amortized: Worst-case running time for any sequence of $n$ operations.
- Example: Starting from an empty stack, any sequence of $n$ push and pop operations takes $O(n)$ primitive computational steps using a resizing array.
-
Average-case analysis, smoothed analysis, competitive analysis (for online algorithms), etc.
asymptotic order of growth
Big O Notation
-
Upper bounds: $f(n)$ is $O(g(n))$ if there exist constants $c \gt 0$ and $n_0 \ge 0$ such that $0 \le f(n) \le c \cdot g(n)$ for all $n \ge n_0$.
-
Ex: $f(n) = 29n^2 + 11n + 5$
-
$f(n)$ is $O(n^2)$
-
$f(n)$ is neither $O(n)$ nor $O(n~\text{log}~n)$.
-
-
Typical usage: Insertion sort makes $O(n^2)$ compares to sort $n$ elements.
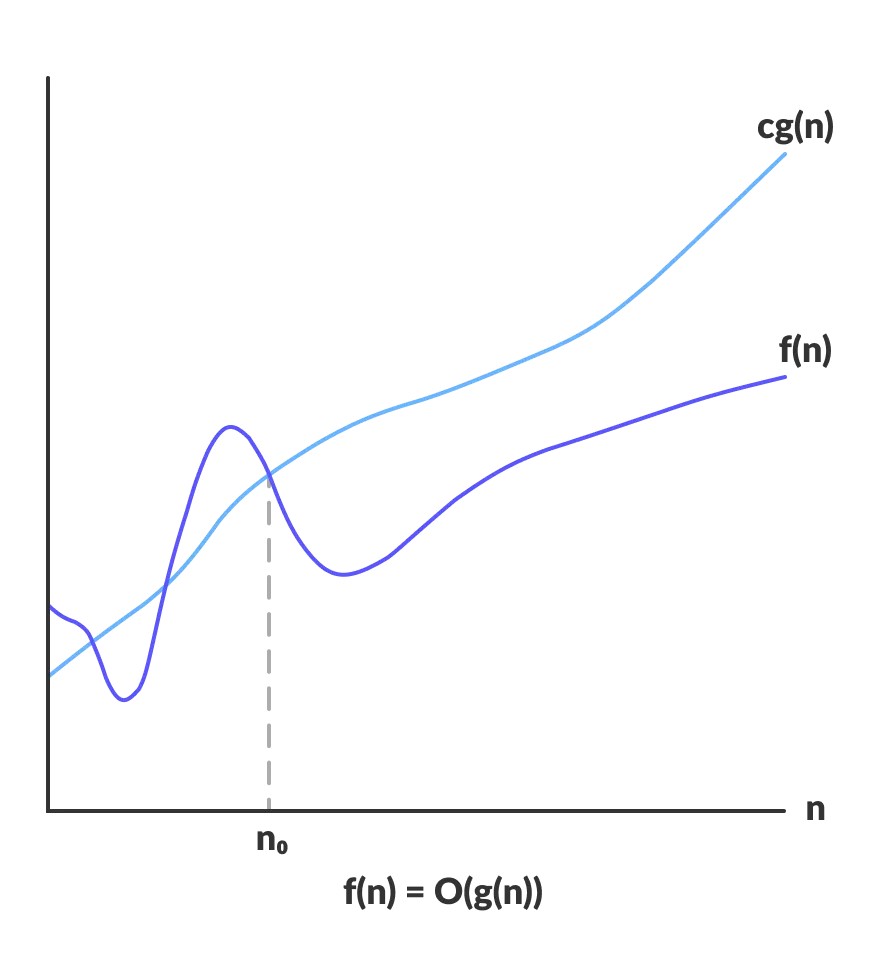
|
|---|
| Sourced from Programiz |
- Notice how $f(n)$ is both greater than and lesser than $g(n)$ before $n_0$, but then after $n_0$ i.e. for all $n \ge n_0$, $f(n) \le g(n)$.
Big O Notational Abuses
-
One-way “equality”: $O(g(n))$ is a set of functions, but we computer scientists often have the nasty habit of writing $f(n) = O(g(n))$ instead of $f(n) \in O(g(n))$
-
Ex. Consider $g_1(n) = 7n^3$ and $g_2(n) = 2n^2$.
-
We have $g_1(n) = O(n^3)$ and $g_2(n) = O(n^3)$.
-
But do not consider $g_1(n) = g_2(n)$, this is just not true.
-
-
-
Domain and codomain. $f$ and $g$ are real-valued functions.
-
The domain is typically the natural numbers: $\mathbf{N} \rightarrow \mathbf{R}$.
-
Sometimes we extend to the reals: $\mathbf{R}_{\ge 0} \rightarrow \mathbf{R}$.
-
-
Remember: It is ok to abuse notation, not ok to misuse it (i.e. draw conclusions through misused notations.)
Big O notation: Properties
-
The “cieling”, if you will, of an algorithm.
-
Reflexivity: $f$ is $O(f)$.
-
Constants: If $f$ is $O(g_1)$ and $f_2$ is $O(g_2)$, then $f_1 f_2$ is $O(g_1 g_2)$.
-
Proof.
-
$\exists~c_1 \gt 0$ and $n_1 \gt 0$ such that $0 \lt f_1(n) \le c_1 \cdot g_1(n)$ for all $n \gt n_1$.
-
$\exists~c_2\gt 0$ and $n_2 \gt 0$ such that $0 \lt f_2(n) \le c_2 \cdot g_2(n)$ for all $n \gt n_2$.
-
Then, $0 \lt f_1(n) \cdot f_2(n) \lt c_1 \cdot c_2 \cdot g_1(n) \cdot g_2(n)$ for all $n \gt \text{ max }(g_1, g_2)$. $\blacksquare$.
-
-
-
Sums: If $f_1$ is $O(g_1)$ and $f_2$ is $O(g_2)$, then $f_1 + f_2$ is $O(\text{ max }(g_1, g_2))$.
-
Transitivity: If $f$ is $O(g)$ and $g$ is $O(h)$, then $f$ is $O(h$).
-
Example: $f(n) = 2n^3 + 10000n^2 + 80n + 4721$ is $O(n^3)$.
Big Omega Notation
-
The “floor”, if you will, of an algorithm.
-
Lower bounds: $f(n)$ is $\Omega (g(n))$ if there exist constants $c \gt 0$ and $n_0 \ge 0$ such that $f(n) \ge c \cdot g(n)\ge 0$ for all $n \ge n_0$.
-
$f(n) = 26n^2 + 4n + 100$.
-
$f(n)$ is both $\Omega(n^2)$ and $\Omega(n)$.
-
$f(n)$ is not $\Omega(n^3)$.
-
-
Typical usage: Any compare-based sorting algorithm requires $\Omega(n~\text{log}~n)$ compares in the worst case.
-
$f(n)$ is $\Omega(g(n))$ iff $g(n)$ is $O(f(n))$. This is the primary relationship between Big O and Big Omega notation.
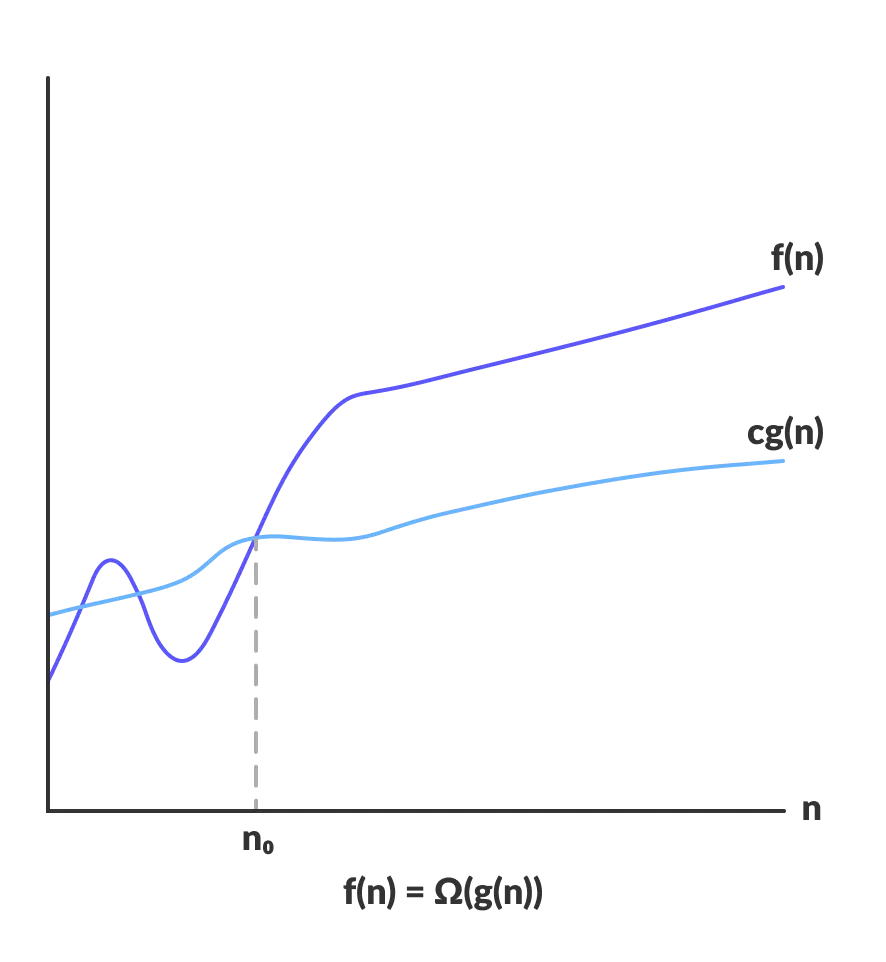
|
|---|
| Sourced from Programiz |
- Notice how $f(n)$ is both greater than and lesser than $g(n)$ before $n_0$, but then after $n_0$ i.e. for all $n \ge n_0$, $f(n) \ge g(n)$.
Big Theta Notation
-
The “room”, if you will, of an algorithm.
-
Tight bounds: $f(n)$ is $\Theta(g(n))$ if there exist constants $c_1 \gt 0,~c_2 \gt 0$, and $n_0 \ge 0$ such that $0 \le c_1 \cdot g(n) \le f(n) \le c_2 \cdot g(n)$ for all $n \ge n_0$.
-
$f(n) = 16x^{2} + 17x + 1$.
-
$f(n)$ is $\Theta(n^2)$, choose $c_1 = 16$, $c_2 = 24$, $n_0 = 1$.
-
$f(n)$ is neither $\Theta(n)$ nor $\Theta(n^3)$..
-
-
Typical usage: Mergesort takes $\Theta(n~\text{log}~n)$ compares to sort $n$ elements.
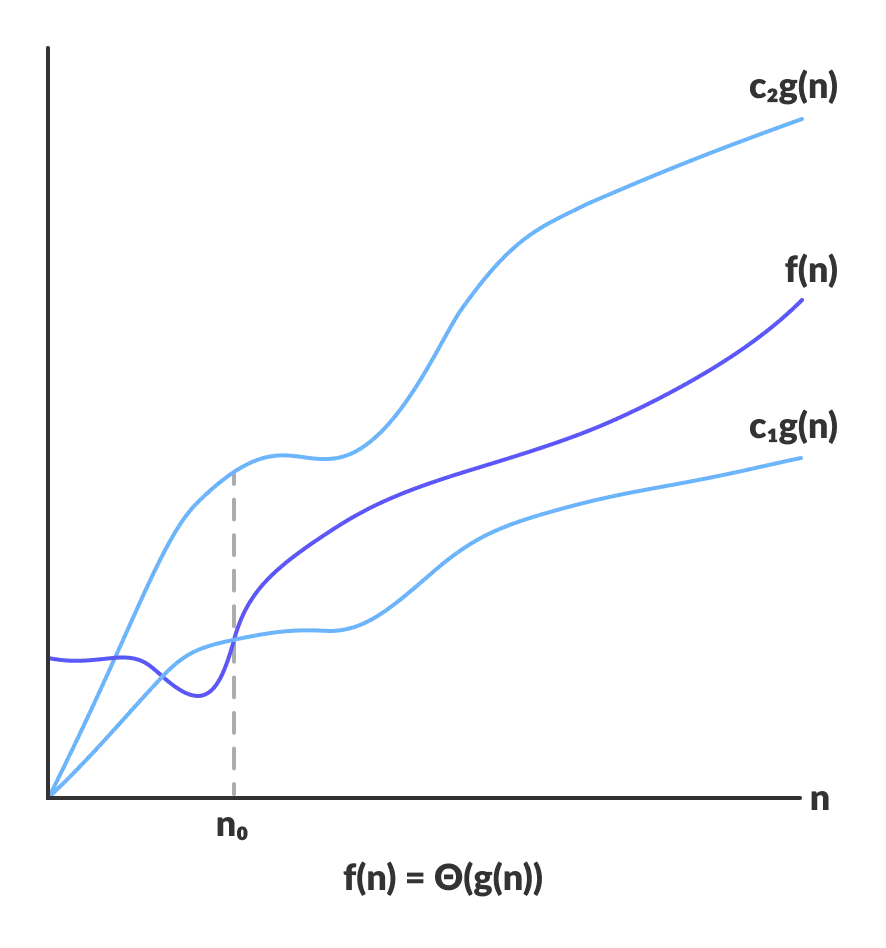
|
|---|
| Sourced from Programiz |
Graphs
Basic Definitions and Applications
Undirected Graphs
Notation: $G = (V, E)$ where:
-
$V =$ nodes (also called vertices).
-
$E =$ edges (also called arcs) between pairs of nodes.
-
Captures “pairwise” relationship between objects.
-
For reference, the graph size parameters used later are: $n = |V|$, $m = |E|$, i.e. $n$ is number of nodes, $m$ is number of edges.
Graph Representation
Adjacency Matrix
An $n$-by-$n$ matrix such that $A_{u,~v} = 1$ if $(u,~v)$ is an edge.
-
Two representations of each edge (i.e. $A_{u,~v}$ and $A_{v,~u}$).
-
Space complexity is $\Theta(n^2)$.
-
Checking if $(u,~v)$ is a valid edge takes $\Theta(1)$ time.
-
Identifying all edges takes $\Theta(n^2)$ time.
Adjacency Lists
Array of lists that are indexed via nodes.
-
Two representations of each edge.
-
Space is $\Theta(m + n)$.
-
Checking if $(u, v)$ is an edge takes $O(degree(u))$ time, where degree is the number of neighbors of $u$.
-
Identifying all edges takes $\Theta(m + n)$ time.
Paths and Connectivity
-
Definition: A path for an undirected graph $G = (V,~E)$ is a sequence of nodes $v_0,~v_1,~...,~v_k$ such that each consecutive pair, $v_{i -1},~v_i$ is joined by a distinct edge $E \in G$.
-
Definition: A path is simple if all nodes are distinct, i.e. no duplicate nodes in the sequence.
-
Definition: An undirected graph is regarded as connected if for every pair of nodes $u$ and $v$ there exists a path between $u$ and $v$. Notice I said a path not an edge.
Cycles
-
Definition: A cycle is a path ($v_1,~v_2,~...,~v_k$) in which $v_1 = v_k$ and $k \ge 2$. This would break down if $k$ equals one.
-
Definition: A cycle is regarded as simple if all nodes are distinct, i.e. no duplicate nodes in the sequence with the exception of $v_1$ and $v_k$.
Trees
-
Definition: An undirected graph is a tree if it is connected and doesn’t contain a cycle.
-
Theorem: Let $G$ be an undirected graph of $n$ nodes. If two of the following are true, the third is implied:
-
$G$ is connected.
-
$G$ doesn’t contain a cycle.
-
$G$ has $n-1$ edges, i.e. $m = n - 1$.
-